Neural Oscillations

While MEEG spectral analysis is as old as EEG existence itself, many tools have been developed over the years.  Since we published the COBIDAS MEEG in 2020, an abundance of papers appeared on this topic - which admittedly the recommendation does not address a lot. Below is a quick review of the 3 papers that summarize best, in my opinion, the current state of the field.

The periodic part

In case you are not familiar with the idea of oscillation, the theory is that groups of neurons produce synchronous and periodic signals leading to observed a rhythmic activity called neural oscillations. There is also evidence that neural oscillations relate to the coordination of neural activity between spatially distant regions in the brain, i.e. connectivity. 

Donoghue et al. EJN 2021 have a great overview of this with analysis recommendations. Do also check the website related to the paper - an incredible resource for all: https://oscillationmethods.github.io/docs/index.html

Capture from the website/notebook simulating signal
decomposition for an oscillation + a period signal

Oscillations come into 2 main forms, the often assumed constant period signal (in blue the figure above) that in theory can be measured at any time (but it is rarely the case) and as bursts (which needs special types of analyses). An additional complication is that oscillations are not necessarily sinusoidal creating harmonics in the spectrums, which can lead to spurious connectivity results. 

Keil et al. Psychophysiology 2022 have provided a set of recommendations to analyse and report on spectral analyses. In their introduction, they also refer to an important distinction among different types of oscillations: 

(i) spontaneous oscillations, which are not related to external stimuli, 

(ii) evoked oscillations, which are elicited and precisely time-locked to the onset of an external stimulus, 

(iii) emitted oscillations, which are time-locked to a stimulus that was expected but then did not occur, and 

(iv) induced oscillations, which are prompted by a stimulus but are not time- and phase-locked to its onset. 

Finally, with the renewed interest in frequency tagging paradigms, it is important to distinguish intrinsic oscillations (emerging dynamics of the brain) from driven oscillations (occurring in response to periodic stimulation).

Aperiodic Signal

MEEG signals have not just oscillatory activity, they also have an aperiodic component (of 1/f type - in red in the figure above), which seems to relate to postsynaptic potentials. In terms of spectral power, this means that there is always non-zero power, whatever frequency one is looking at. A great point made by Donoghe: any spectral analysis will return a value at a given frequency because of this aperiodic signal, this does not mean there is an oscillation - also pointing out the danger of narrow-band filtering.  

The aperiodic signal is also dynamic! like oscillations, that part of the spectrum has been shown to vary with cognition, states, disease, etc .. and thus can be studied on its own, although a good analysis would look at both aspects of the signal (I wonder if anyone has look into how these interact at all, a quick google search did not give me any results? please leave some reference in the comments if you know of any paper like that)

Pink noise illustration

Gerster et al. NeuroInformatics 2022 present a careful analysis and overview of methods designed to assess 1/f^𝜷 signal, in particular, evaluate the exponent 𝜷 - which determines the slope of the aperiodic signal with challenges for any methods: spectral plateau, hidden low-frequency oscillations and overlapping peaks.

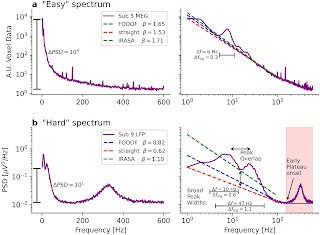Figure 8 from Gerster et al. illustrating
challenges in PDS analyses

In conclusion, as always, not one method fits all purposes and careful considerations should be taken when looking at the power spectrum. I believe those 3 recent papers provide an excellent starting point for any analysis in this domain.