GLM single trial weighting for EEG

Weighting single trials in EEG for better precision 

It has been may years since I tried to implement a single trial weighted least squares in LIMO tools. The core idea is to have weights that capture trial dynamics - and that was developed more than 7 years ago. Armed with this algorithm, we can just plug that in to a GLM and that's it, more precision in the parameter estimates (i.e. reflects better the truth) and possibly better group level results. The preprint is finally out! Let me tell you why I think this is a useful approach, and what made it so hard to implement.

Single Trial Weighting

Before looking at how we compute this, let's think of a standard weighting scheme: we look at how data points are distributed to obtain weights, say using the inverse of the variance, and we compute the weighted mean, or parameter estimates in a GLM - the idea is simple, the farther away from the bulk, the less weight.

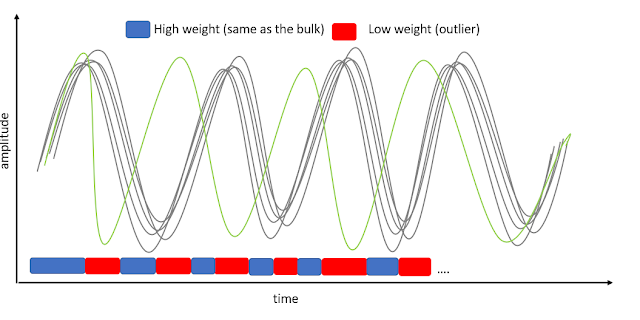
What happen if you use a naive weighting to time courses? Let's look at a trial slightly out-of-phase (figure 1). At each time point, we look at deviations and apply weights. While the result is a better approximation of the truth, time points are seen as an alternation of 'good' then 'bad' data. Physiologically, this is weird - neurons don't compute things independently at each time point, this is clearly an auto-regressive process - we just cannot ignore that.

Figure 1. Example of a trial out-of-phase (green) compared to the bulk (dark grey). If weighting is computed independently at each time point, we observe an alternation of high and low weights - which would indicate that neural activity is sometimes different and sometimes the same as for other trials.

Our approach assign weights based on the whole trial temporal profile, and how if differs from the bulk. For that we use the Principle Component Projection method developed by Filzmoser et al. (2008). The result are means or parameter estimates that approximate the truth just as well as the naive approach but with a scheme that is biologically meaningful. If the result is the same who cares? well, it looks like the same, but isn't - check the preprint, the type of noise for instance has different impact and this matters. 

Just use weights into a GLM, it's easy they said ...

You might think, once you have weights just plug them in your GLM and compute Weighted Least Squares.  This is what I did, and it worked - parameters estimates were less influences by those outlying trials. So why 7 years? because while estimation was better, I just couldn't get the inference to work. You might argue that 1st level/subject inference isn't that interesting so who cares. I care. This isn't satisfying to have half baked solutions. It took 7 years because life takes over and you get busy into other stuffs, since your ideas keeps failing; but I kept at it - occasionally testing something different. 

The difficulty for inference is that LIMO tools like other software use a massive univariate approach, i.e. consider each data independently, then do a multiple comparison correction based on clustering (cluster mass and tfce) - but the weighting doesn't! and that led to crazy false positive rates, until I found the right way to resample the data (turns out you cannot center the data for the null, just break the link between X and Y; and you should reuse the weights rather than compute new ones each time ... ah and of course there are a few other tricks like adjusting your mean squared error since the hyperplane doesn't overfit anymore, you must be less than ordinary least squares, just to make things more interesting ...).

 And so it works

Having solved that subject inference issue, we can move on and pool those parameter estimates and compute group level statistics. At 1st glance, great, more statistical power, more effects detected (figure 2) - thanks to more precision which can reduce between subject variance. 

Figure 2. Group results from Wakeman and Henson (2015) face experiment using 1st level OLS parameter estimates (top) vs. 1st level WLS parameter estimates (bottom) illustrating the discrepancy of more statistical power (left) despite smaller effect sizes (right).  

Digging deeper, you'll see it's more complicated because overall effects are weaker (check the scales of those maps ... ). It's not totally surprising if you think you got rid of most influential trials (but I agree this could have went the other direction). Weaker effects but more statistical power? well the relative size of real effects compared to space/time areas where nothing happen is larger, that is the distributions are right skewed - and since resampling under the null gives very similar cluster masses and tfce maxima across methods and right skewed maps cluster more, we end-up with more statistical power at the group level when using subject level weighted least squares than using standard ordinary least squares. 

I can see other applications than GLM-EEG, basically we have weights for profiles (temporal/spectral) acting as variance stabilizers, there must be a few applications out there that can make use of that.  

As always, nothing is simple in research - but isn't why we love it?